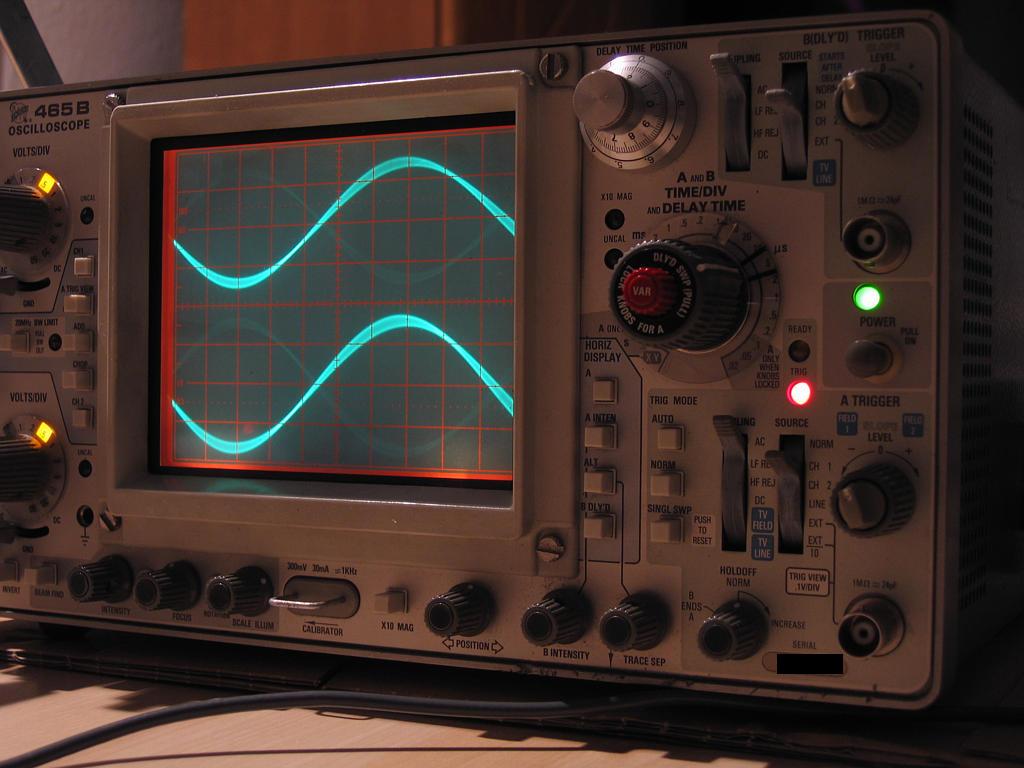
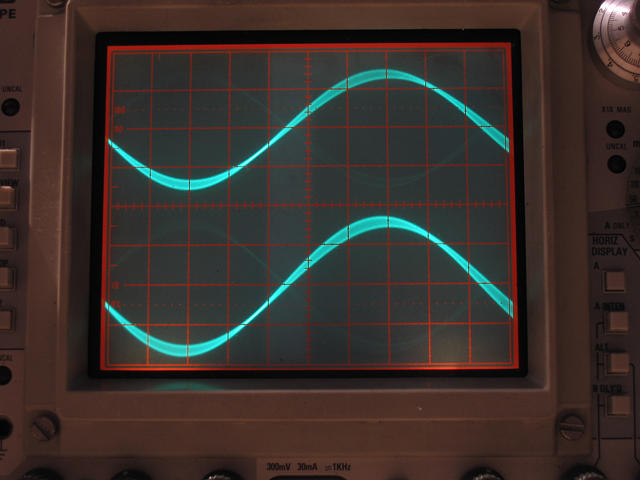
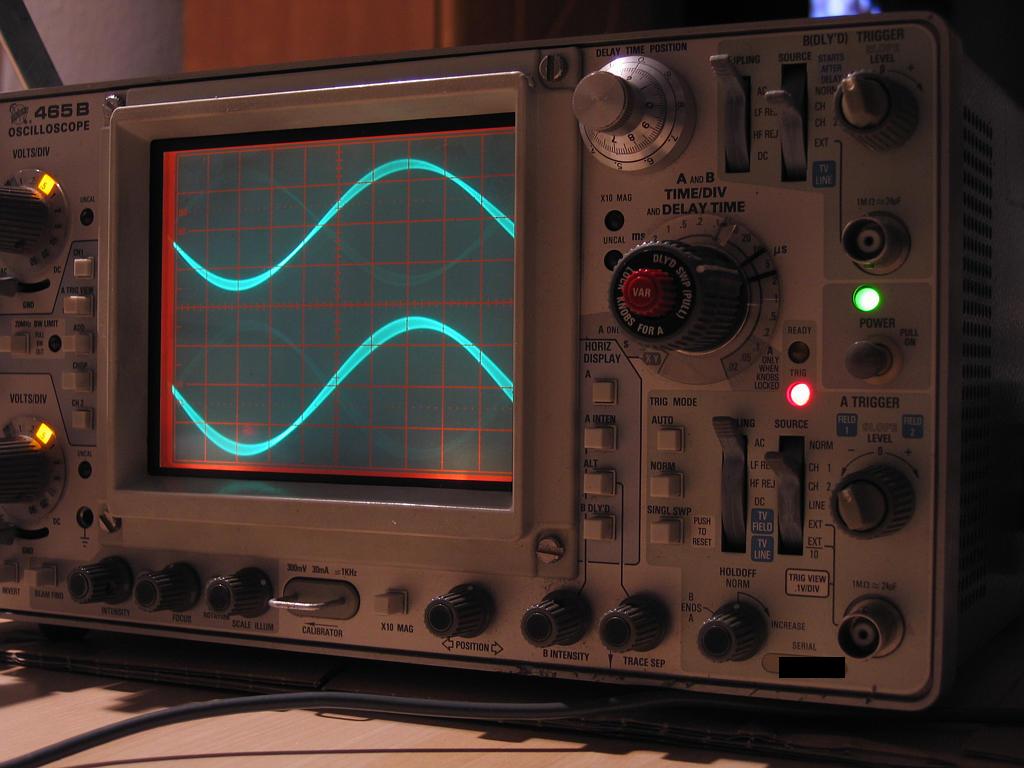
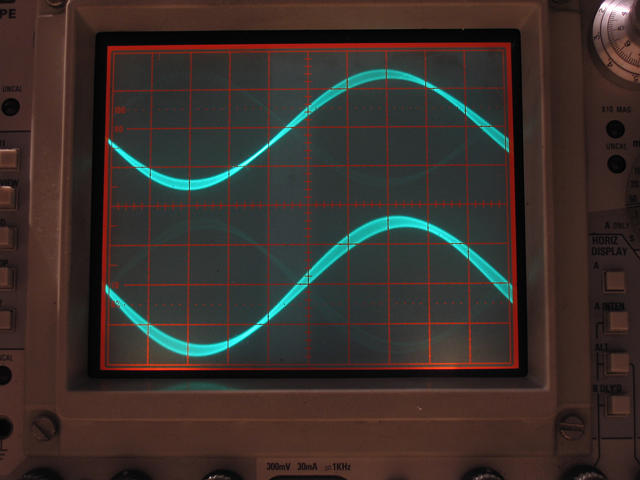
To show this in practice we simply generate a sinewave on the left channel and a time-shifted sinewave on the right channel and see if this timing difference can be reproduced by the digital system.
First let's recall the basic equation of a sinewave: x(t) = sin (2 · π · f · t). On the other channel we use a time-shifted sine by the amount of Δt with y(t) = sin (2 · π · f · (t + Δt)). Many literature on human hearing demands an interchannel timing difference as low as 10 µs or even 2 µs to be inaudible (which corresponds to an incident angle of ca. 0.5°, see for example Blauert). We want to show that this time-shift is easily achievable with common systems (for example with any ordinary real cheap CD-player), so we choose Δt = 2 µs for our test.
With the above definition we generate a sinewave with a frequency of 19.997 kHz at a sampling-rate of 44.1 kHz and a time-shifted signal by 2 µs with the same frequency. The signal is played back with an old Soundblaster AWE 32 soundcard and displayed with an even older (and fully analogue) Tektronix 465B scope. The scope was not touched during the shots, all settings remain the same.
Time-deviation is 5 µs/div (see big knob on the right-hand side of the scope) so you will notice that the waveform on the lower picture in fact shifts 2 µs relative to the waveform on the upper picture.
(move the mouse pointer over an image to see the shifted version; click on any image to see a larger version)

|

|
|
|